L’équilibre de marché résulte de la confrontation de l’offre et de la demande. Nous verrons tout d’abord comment cet équilibre se réalise sur chacun des marchés (équilibre partiel) puis nous évoquerons la notion d’équilibre général : il s’agira alors d’évoquer l’interdépendance des marchés et se demander dans quelle mesure le marché assure l’optimum, c’est-à-dire la meilleure solution possible.

 I) L’équilibre partiel.

A) Quelques hypothèses .

Pour que la régulation par les prix soit optimale et donc pour que l’équilibre de marché soit assuré il faut que les conditions de concurrence pure et parfaite soient respectées. La concurrence sera qualifiée de pure et parfaite quand les 5 conditions suivantes seront respectées :

1. L’atomicité du marché.

Le marché doit être formé d’un grand nombre de firmes et d’un grand nombre de consommateurs. Le « grand nombre » veut dire que chaque entreprise doit avoir une taille suffisamment petite pour ne représenter qu’une très faible part du marché. Nous dirions aujourd’hui que chaque firme est une PME. Il en découle que la variation de l’offre de la part d’un producteur ne peut significativement modifier les conditions d’offre et de demande du marché. Ultime conséquence de cette caractéristique : aucune firme n’a d’influence sur le prix du marché. Cette impossibilité d’influer sensiblement sur le prix est qualifiée d’absence de pouvoir de marché. On dit également que l’entreprise est un price taker. En 1848, J.S. Mill écrivait que la concurrence est une situation où « il ne peut y avoir, pour le même produit, de qualité identique, deux prix sur le même marché ».

2. L’homogénéité du produit :

Tous les produits des fabricants d’une même industrie sont identiques. La différenciation, la publicité et toute autre forme de marketing sont inconnues, et les consommateurs n’ont aucune autre raison que le prix pour choisir un vendeur plutôt qu’un autre.

3. Libre entrée dans la branche (ou l’industrie) :

Il n’existe pas de barrière juridique ou réglementaire (brevets de fabrication...) à l’entrée de nouveaux concurrents dans la production du bien considéré. Il n’existe pas plus de barrières techniques ou financières (importance du capital fixe...). La concurrence pure exclut par hypothèse toute barrière, à l’entrée et à la sortie, quelle que soit sa nature. Cette hypothèse joue un rôle fondamental dans la disparition des profits anormaux, l’une des vertus majeures de la concurrence

4. La transparence du marché.

La transparence consiste en une information totale pour le consommateur, le travailleur et la firme. L’information est parfaite et les agents savent l’analyser ; ils peuvent choisir en connaissance de cause la situation optimale. Et, de ce fait, il ne peut y avoir qu’un seul prix.

5. La parfaite mobilité des facteurs de production :

Ce terme recouvre la mobilité totale des facteurs de production, travail et capital. Les salariés peuvent changer de branche à leur guise. Les facteurs de production se dirigent vers les emplois où on en tire le meilleur parti. Lorsque l’une de ces hypothèses n’est pas satisfaite on parle de concurrence imparfaite.

B) La détermination de l’équilibre en courte et en longue période

La « courte période » est la période durant laquelle la production de la firme peut se modifier mais où la capacité de production, les équipements sont fixes ; alors que durant la « longue période » la capacité de production de la firme peut être modifiée.

1) L’équilibre de courte période.

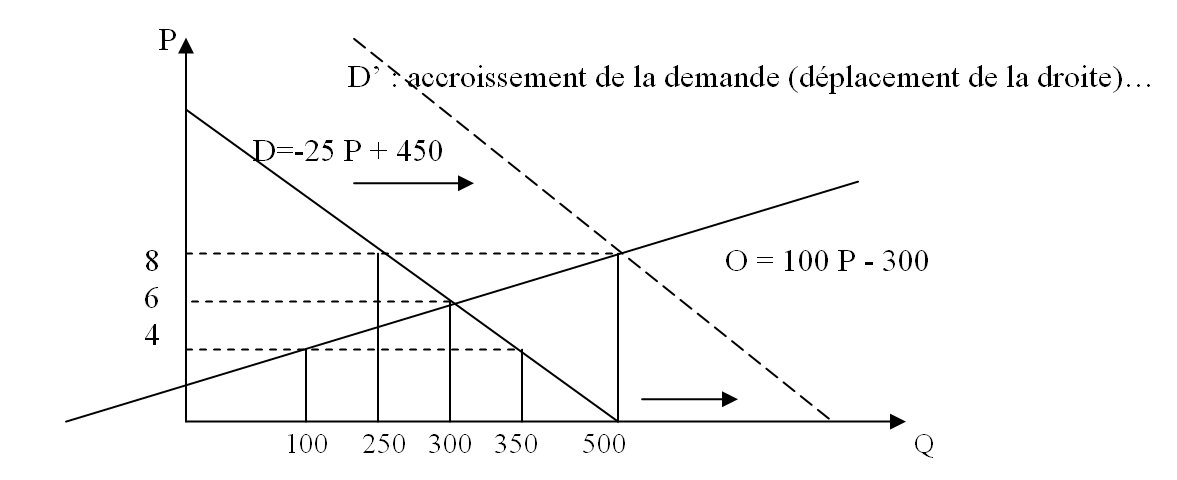
L’échange ne se fait qu’à l’équilibre et l’équilibre est atteint à l’intersection de la courbe d’offre globale et de la courbe de demande globale. La solution est unique, il y a un seul prix et une seule quantité. Elle satisfait de la meilleure façon possible à la fois les désirs des acheteurs et ceux des vendeurs. Comment cet équilibre est-il atteint ? C’est à ce niveau qu’intervient le « commissaire priseur », cette intervention est nécessaire pour assurer l’unicité du prix. Acheteurs et vendeurs se présentent sur le marché ; les quantités achetées et vendues sont inconnues puisque offre et demande dépendent du prix du bien qui n’est pas encore fixé. Les fonctions d’offre et de demande sont connues, non le niveau ; ??? cela suppose que la production est instantanée, que les producteurs arrivent sur le marché sans avoir pris leurs décisions de production. L’équilibre, point d’intersection des courbes d’offre et de demande, est atteint grâce à l’action du commissaire-priseur et au jeu de contrats successivement passés et rompus à des prix éloignés de l’équilibre.

Si le prix est inférieur à 6 euros, par exemple 4, il y a un excès de demande par rapport à l’offre (D= 350>O=100). Toute la demande n’est pas satisfaite à ce prix. Il y a « concurrence » entre acheteurs et certains sont prêts à faire monter les enchères et ainsi provoquer une augmentation de l’offre jusqu’au moment où le prix rejoint le prix d’équilibre de 6 euros, grâce à l’action du commissaire-priseur. Cette hausse des prix a provoqué une augmentation de l’offre et une diminution de la demande (déplacement sur la courbe). La courbe d’offre et la courbe de demande peuvent se déplacer : la première à la suite de modifications dans la fonction de production de chacun des producteurs (conséquence par exemple d’un progrès technique, d’une modification dans les combinaisons productives), la seconde en écho aux changements dans la fonction d’utilité d’un ou plusieurs consommateurs (modification dans la mode, action de la publicité...) ; enfin l’une et l’autre peuvent être affectée par des modifications dans le niveau des contraintes jouant au niveau de chaque agent individuel (ressources disponibles, prix des facteurs utilisés ou des biens consommés...).

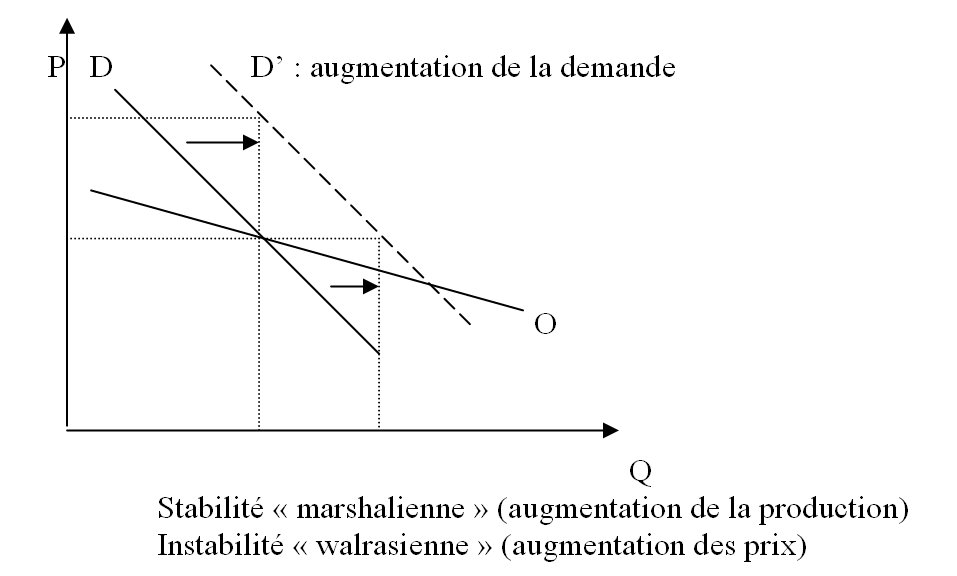
Le prix d’équilibre est-il stable ? On dira que l’équilibre est stable si une perturbation qui provoque un déplacement de la courbe d’offre ou de demande est suivie d’un retour à l’équilibre (différent de l’équilibre initial évidemment).Lorsque l’offre et la demande sont « normales » la modalité d’ajustement retenue importe peu : l’équilibre est stable aussi bien au sens de Walras (ajustement par les prix : ex : l’excès de demande => hausse des prix) qu’au sens de Marshall (ajustement par les quantités : ex : excès de demande =>hausse de la production).Lorsque l’une des deux courbes est anormale, l’équilibre n’est plus nécessairement stable ; tout dépend du mode d’ajustement et de la pente respective des deux courbes. Exemple : Offre anormale (offre fonction décroissante du prix : la baisse des prix peut entraîner un accroissement de la quantité offerte pour obtenir le maintien de la recette)

Lorsque les deux courbes sont anormales (la demande est fonction croissante des prix : ex paradoxe de Giffen, biens inférieurs ; l’augmentation du prix de la pomme de terre rend les consommateurs déjà très démunis encore plus pauvres, ce qui les contraint pour survivre à acheter davantage...du seul bien qu’ils puissent acheter avec leur misérables ressources ; l’effet de revenu est supérieur à l’effet de substitution) Il y a alors instabilité complète quel que soit le mode d’ajustement retenu (marshalien ou walrasien). Le retour à l’équilibre suite à une perturbation est fonction du type de comportement qui prévaut sur le marché ; le retour à l’équilibre n’est pas automatique, cela dépend du type de courbe et du type de réponse de la part des coéchangistes. 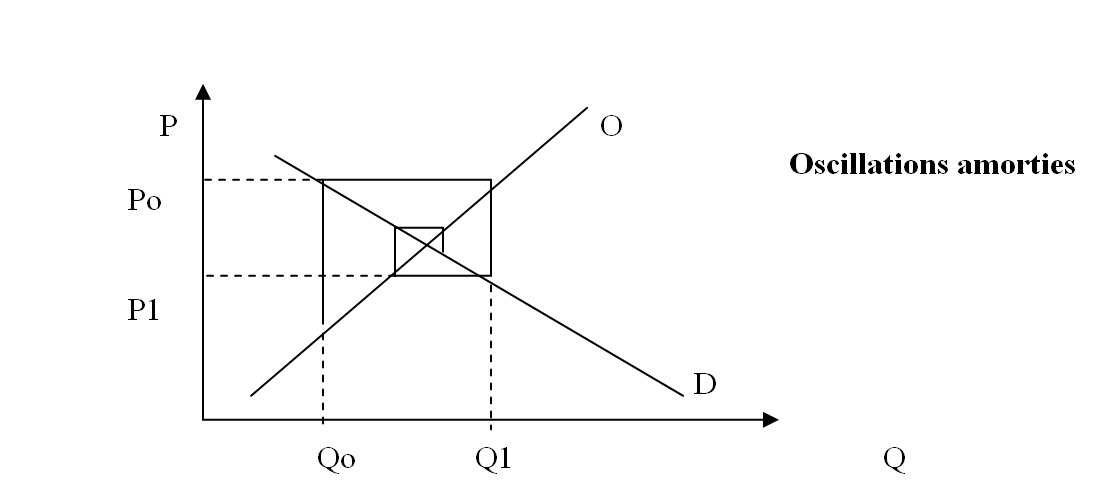Que se passe-t-il si l’on prend en compte les délais d’ajustement ? La production demande...du temps. Les biens agricoles (blé, élevage de porc...) constituent de bonnes illustrations : les plans de production sont faits sur le prix du marché à l’automne ; la production ne se matérialise qu’un an plus tard. On a donc, en supposant pour simplifier que les fonctions sont linéaires : Ot = Apt-1 + B et Dt = apt + b.On suppose en outre que la production est intégralement vendue (il n’y a pas de possibilité de stockage). On se situe donc ici dans le cadre de la « période de marché » ou « période ultra courte » trop brève pour que la production puisse varier ; les modifications dans la production ne se produisant que d’une période à l’autre.

Le niveau du prix fluctue de période en période, pour converger vers le point d’équilibre indiqué par le point d’intersection des deux courbes.Ce processus continu forme une « toile d’araignée » (cobweb en anglais) sur la figure.Mais lorsque la courbe de la demande est en valeur absolue supérieure à la courbe d’offre les fluctuations du prix tendent à devenir de plus en plus grandes, à s’éloigner du prix d’équilibre. Dans le cas d’équilibre dynamique avec adaptation retardée des producteurs, le modèle de la « toile d’araignée » fait apparaître que l’équilibre du marché n’est stable que si la pente de la courbe d’offre est supérieure à la valeur absolue de la pente de la courbe de demande.

2) L’équilibre de longue période.

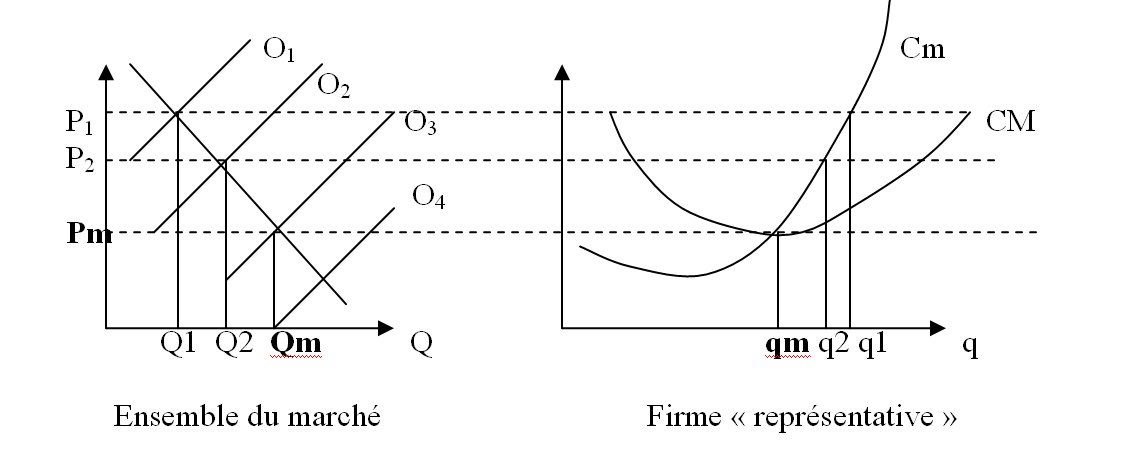
On suppose qu’il existe un prix d’équilibre unique et stable (la courbe d’offre et la courbe de demande sont normales).Le prix de marché s’impose à l’entreprise, c’est l’hypothèse de concurrence parfaite qui implique l’atomicité de chacun des producteurs ; le producteur ne peut en courte période qu’ajuster le niveau de production. C’est ainsi qu’il va maximiser son profit.

Supposons que toutes les entreprises produisent dans les mêmes conditions ; les courbes de coût de chacune d’elles ont exactement la même forme. Pour P1 chaque entreprise réalise un profit supérieur à la normale, un superprofit puisque le prix est supérieur au coût moyen (qui inclut, rappelons-le, la rémunération normale de l’ensemble des facteurs de production, y compris celle du chef d’entreprise...). Toutes les entreprises réalisent donc des profits supérieurs au « profit normal ». De nouveaux chefs d’entreprise sont en conséquence, incités à entrer sur le marché. D’après l’hypothèse de « libre-entrée » ils peuvent le faire et produire le même bien (homogène) dans les mêmes conditions de coût. Les nouveaux producteurs vont ajouter leur offre à l’offre déjà existante et il en résultera un déplacement de la courbe d’offre vers la droite d’où un nouveau prix d’équilibre et une diminution du niveau de production de chaque entreprise. Tant que des profits « anormaux » seront réalisés, de nouveaux producteurs continueront d’entrer sur le marché jusqu’à ce que le prix du marché annule les « superprofits ». Le prix, toujours égal au coût marginal, est égal au coût moyen minimum.Si un nombre excessif de producteurs est entré sur le marché, le prix du marché est insuffisant et toutes les entreprises subissent des pertes ; certaines entreprises vont se retirer, l’offre globale diminue, la courbe d’offre globale va se déplacer vers la gauche jusqu’à ce que soit obtenu le prix pour lequel les pertes et...les profits soient nuls A l’équilibre de longue période, la demande est égale à l’offre et tous les profits (« superprofits ») sont nuls.

Supposons maintenant des conditions de coût différentes (les équipements sont de taille et d’efficacité différentes, les chefs d’entreprise n’ont pas nécessairement tous les mêmes talents...).Si la demande est forte, le prix du marché est élevé et toutes les entreprises réalisent des « superprofits » ; si elle diminue (ou que de nouveaux producteurs attirés par l’existence de profits anormaux entrent dans la branche) , seules les entreprises aux courbes de coût les plus performantes resteront sur le marché. Cela signifie que l’on retrouve la similitude des courbes de coût non plus comme hypothèse mais comme conséquence, comme aboutissement logique du processus d’élimination des entreprises les moins productives.

 II) Equilibre général et optimum

A) Équilibre général et interdépendance des marchés

L’idée de l’équilibre général soulève de nombreuses questions : quel effet la modification d’une variable sur un marché a-t-elle sur les autres marchés ? L’équilibre sur chacun des marchés est-il possible ? S’il existe est-il unique ? Y a-t-il une autorégulation par les prix qui permette de retourner à l’équilibre sur tous les marchés interdépendants ? Le premier à avoir cherché à démontrer l’impossibilité d’un déséquilibre durable entre l’offre et la demande est J.B. Say qui affirme que « l’offre crée sa propre demande ». En effet, la production, lorsqu’elle est vendue, se transforme en revenus qui servent à acheter la production. « Les produits s’échangent contre les produits » et la demande est forcément égale à l’offre. La loi de Say est donc une première présentation de l’équilibre général dans le sens où plusieurs marchés sont concernés. « C’est parce que la production des produits manquants a souffert, que les produits surabondants ne trouvent point de débit, et que leur valeur s’est altérée. En termes vulgaires, beaucoup de gens ont moins acheté, parce qu’ils ont moins gagné ; et ils ont moins gagné, parce qu’ils ont trouvé des difficultés dans l’emploi de leurs moyens de production, ou bien parce que ces moyens leur ont manqué. Aussi l’on peut remarquer que les temps où certaines denrées ne se vendent pas bien, sont précisément ceux où d’autres denrées montent à des prix excessifs ; et comme ces prix élevés seraient des motifs pour en favoriser la production, il faut que des causes majeures ou des moyens violents, comme des désastres naturels ou politiques, l’avidité ou l’impéritie des gouvernements, maintiennent forcément cette pénurie d’un côté, qui cause un engorgement de l’autre. Cette cause de maladie politique vient-elle à cesser, les moyens de production se portent vers les canaux vacants, et le produit de ceux-ci absorbe le trop-plein des autres ; l’équilibre se rétablit, et cesserait rarement d’exister, si les moyens de production étaient toujours laissés à leur entière liberté » J.B. Say « Traité d’économie politique » 1803

Léon Walras va tenter de traiter rigoureusement la double question de l’existence et de la stabilité d’un équilibre général, en posant le problème sous une forme mathématique élémentaire. Il s’agit de savoir si le système d’équations multiples constitué par les équations d’équilibre.

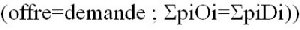
a une solution.

Les mathématiques enseignent alors qu’une condition nécessaire à l’existence d’une telle solution est de disposer d’autant d’équations que d’inconnues à déterminer. Pour résoudre ce problème Walras introduit un nouveau concept, le numéraire ; un bien choisi comme unité de compte. Les prix de tous les autres biens, ou facteurs sont exprimés par le prix du numéraire, lequel est égal à 1.L’intérêt de cette démarche est de réduire le nombre d’inconnues d’une unité et le système devient déterminé. Il a une solution (mais une solution mathématique).Pour autant aboutit-il à l’équilibre général (une solution ayant un sens économique) ? Walras l’affirme : si l’économie est organisée comme un ensemble de marchés concurrentiels, où l’on peut instantanément renégocier les prix jusqu’au moment où l’on n’échange qu’au prix d’équilibre, un équilibre général est possible et susceptible, en cas de choc quelconque , d’être automatiquement rétabli par les forces du marché. Mais il ne put le démontrer. Et il faudra attendre les travaux d’économistes contemporains, comme K. Arrow et G. Debreu dans les années 1950 ; pour mettre en évidence, et sous certaines conditions, un équilibre économique général.

Grâce à un nombre très restreint d’hypothèses, ils démontrent l’existence de cet équilibre général :

• les marchés sont en concurrence pure et parfaite et sont complets (pour tous les biens présents mais aussi les biens futurs).
• Chaque ménage dispose d’une dotation initiale qui lui permet de survivre sans faire d’échanges (la fonction de demande est donc bornée).
• Les préférences sont convexes (cette convexité permet à la fonction de demande d’être continue).
• Absence de coûts fixes. Les rendements d’échelle sont constants ou décroissants (la fonction d’offre est donc une fonction bornée et continue).

A ces conditions, non seulement l’équilibre général est possible, mais en plus il assure l’optimum de Pareto. Mais si la démonstration d’existence montre que l’équilibre général peut exister, elle ne dit pas si après perturbation, grâce aux seuls échanges librement consentis par les agents et à la flexibilité des prix, on converge vers l’équilibre. Ce problème est celui de la stabilité de l’équilibre général ; le théorème de Sonnenschein-Mantel-Debreu (1973-1974) montre que la stabilité de l’équilibre n’est pas garantie, même lorsque les différentes hypothèses sont réunies. L’équilibre général « existe », mais il n’a aucune raison d’émerger naturellement.

B. Bien-être et optimum de Pareto

On aborde ici le cœur de l’aspect normatif de la microéconomie. Que le fonctionnement concurrentiel conduise à un équilibre général ne suffit pas à montrer que ce mode d’organisation est le meilleur possible. Un second pas doit être fait dans ce sens, en définissant un critère permettant de juger de cette efficacité. C’est l’objet de la théorie du bien-être.L’économie du bien-être a pour premier objectif de déterminer, parmi plusieurs états de l’économie lequel est le meilleur ; elle cherche en outre à indiquer les règles à mettre en œuvre pour parvenir à cet objectif.Depuis Adam Smith, la notion d’intérêt général est au cœur de l’économie politique ; un des fondements de la doctrine libérale est en effet l’agrégation harmonieuse des comportements individuels. Ainsi, Smith explique, par sa notion de « main invisible », que chaque individu, en recherchant son intérêt propre, œuvre non intentionnellement pour l’intérêt général qui est défini implicitement comme la somme des intérêts particuliers. Aucun économiste avant Vilfredo Pareto n’avait réellement et précisément cherché à définir cet intérêt général, chacun considérant que cette définition allait d’elle-même. Selon Pareto, l’optimum est « le plus grand bien-être possible pour les individus de la collectivité ». Le bien-être de la société dépend certes du niveau de satisfaction, d’utilité, obtenu par chaque individu mais il n’en est pas la somme. Les comparaisons interpersonnelles des utilités sont impossibles : on ne saurait déterminer de façon objective si un individu A ou B tire une satisfaction plus grande de la consommation d’un ensemble de biens donné (l’utilité étant ordinale et non pas cardinale) Pareto affirme qu’une situation n’est pas optimale s’il est possible d’augmenter le bien-être de tous les individus ou même s’il est possible d’augmenter le bien-être de certains individus. Si, en revanche, on ne peut augmenter le bien-être de certains individus qu’en diminuant celui d’autres individus, l’optimum est très certainement atteint. L’état optimal de l’économie est donc, selon Pareto, la situation dans laquelle il n’est pas possible d’augmenter la satisfaction d’un individu sans diminuer celle d’au moins un autre individu.

1. La multiplicité des optimums au sens de Pareto

Le critère de Pareto permet de classer les différents états possibles de l’économie en, d’une part, les états optimaux et, d’autre part, les états sous-optimaux (non-efficient). Il admet un grand nombre d’états optimaux et il ne permet pas d’opérer un choix entre les différentes situations optimales ; elles sont toutes équivalentes. L’intérêt (limité) de la règle est de permettre de définir des situations qui sont non-optimales, non-efficientes, qui sont des situations de gaspillage que l’on doit éliminer.La définition de l’optimum est assez vague et de nombreuses situations peuvent être jugées optimales, ne serait-ce que parce qu’il est extrêmement rare qu’absolument aucun individu ne perde lors d’une modification économique. Or, Pareto affirme bien qu’il suffit qu’un seul individu voit baisser son ophélimité (utilité) pour que l’on s’éloigne de l’optimum. Par exemple, on a souvent affirmé que la liberté des échanges est positive et améliore le bien-être parce qu’on considère qu’elle accroît l’efficacité économique et que les pertes que subissent certains producteurs sont largement compensées par les gains de l’ensemble de la collectivité. Pourtant Pareto affirme que « si ce petit mouvement fait augmenter le bien-être de certains individus et diminuer celui d’autres, on ne peut plus affirmer qu’il est avantageux à toute la collectivité d’effectuer ce mouvement ».Le critère de Pareto permet de justifier et de laisser perdurer des situations qui ne paraissent pas équitables d’un point de vue social ; c’est le cas, par exemple, d’une société qui serait composée d’un seul individu riche et de nombreuses personnes pauvres ; on ne peut pas transférer une partie de la richesse du premier vers les seconds puisque le riche verrait diminuer son utilité.

Une définition plus précise de l’optimum aurait été de considérer qu’une situation économique est optimale lorsque l’on ne peut pas améliorer la satisfaction d’un individu sans détériorer celle d’au moins un autre individu dans une proportion égale ou supérieure. Cette nouvelle définition réduit énormément le nombre de situations optimales et permet de préciser ce qu’est un optimum. Pareto n’a pas opté pour une telle définition parce qu’il considère que le degré d’utilité n’est pas mesurable ; l’individu peut seulement savoir si une situation lui procure plus ou moins d’utilité qu’une autre situation ; il est impossible de comparer les utilités de plusieurs individus. Ainsi, c’est pour éviter de recourir à des comparaisons d’utilité interpersonnelles, qui seraient contraires à sa conception de l’ophélimité, que Pareto refuse d’évaluer les changements de situations qui améliorent la situation de certains mais qui détériorent la situation d’autres.

2 Les conditions de réalisation

À quelles conditions l’optimum de Pareto est-il atteint ? Pareto n’a pas lui-même développé les conditions de réalisation de l’optimum, mais cela fut fait plus tardivement en 1938 et 1939 par Bergson et par Hicks (cf. « Boîte d’Edgeworth » dans les livres de microéconomie)

• les facteurs de production doivent être utilisés de façon optimale et donc les taux marginaux de substitution technique (taux auquel un facteur de production peut être substitué à un autre en conservant le même niveau de production) doivent être identiques pour toutes les entreprises ; s’ils ne le sont pas, cela signifie que, dans une situation donnée, deux entreprises pourraient augmenter leur production en s’échangeant des facteurs de production ; on ne serait pas alors dans une situation optimale ;
• les biens doivent être répartis de façon optimale entre les ménages et donc les taux marginaux de substitution (quantité d’un bien qui suffit à dédommager le consommateur de la perte d’une unité de l’autre bien) de deux biens quelconques doivent être identiques pour tous les ménages ; sinon, il existe une opportunité d’échange inexploitée,
• il faut une répartition optimale de la production globale entre les biens : le taux marginal de transformation (quantité d’un produit que la collectivité doit sacrifier pour produire un autre produit (par exemple, si l’on veut produire une table en plus, il faut produire trois chaises en moins) doit être identique pour deux produits quelconques au taux marginal de substitution.

Grâce à la flexibilité des prix et à la mobilité des facteurs de production, le marché, en situation de concurrence pure et parfaite, permet de réunir ces différentes conditions ; il devrait donc offrir un optimum au sens de Pareto. En effet, si la concurrence parfaite règne entre les consommateurs, un consommateur maximise son utilité si son taux marginal de substitution entre deux biens est égal au rapport des prix relatifs. Comme les prix sont dans un système de concurrence parfaite les mêmes pour tous les consommateurs, les TMS entre biens sont les mêmes pour tous les consommateurs. Cette égalité qui résulte de la CPP assure que la répartition des biens entre consommateurs est optimale au sens de Pareto.Les prolongements de l’économie du bien-être, notamment ceux de Pigou, mettent en évidence la nécessité de l’intervention de l’État dans certains cas (externalités, biens collectifs...) pour atteindre, ou tout au moins se rapprocher, de l’optimum. L’optimum de Pareto au sens strict admet de nombreuses situations. Si, en revanche, on accepte une définition plus précise de l’optimum (une situation économique est optimale lorsque l’on ne peut pas améliorer la satisfaction d’un individu sans détériorer celle d’au moins un autre individu dans une proportion égale ou supérieure (utilité cardinale)) celui-ci devient unique. A partir de ce moment, il est possible de caractériser différentes situations en fonction de leur proximité par rapport à cet optimum. Ainsi, les optimums de second rang caractérisent des situations qui sont les meilleures possibles compte tenu de la présence de certaines contraintes.

 Bibliographie

• Microéconomie, G. Abraham-Frois, Economica.
• Analyse microéconomique, J. Lecaillon Cujas.
• Découverte de la microéconomie, Cahiers Français, n° ;254.
• Microéconomie, Marc Montoussé, Isabelle Waquet, Bréal.
• Initiation à la microéconomie, Bernard Bernier, Henri-Louis Védié, Dunod.
• Introduction à la microéconomie, G. Rotillon, La découverte.
• La nouvelle microéconomie, P. Cahuc, La découverte.
• L’économie néoclassique, B.Guerrien, La découverte.
• Fondements d’économie industrielle, Yves Morvan. Economica.
• L’économie de marché, R. Guesnerie Dominos, Flammarion.
• Economie de la réglementation. F. Lévêque La découverte.

Pour télécharger cet article au format pdf, cliquez sur le lien ci-dessous :